[previous] [home] [search] Fopra of Marcus Hutter [contact] [up] [next] 

F O R T G E S C H R I T T E N E N P R A K T I K U M

H E B B - N E T Z & R E I N F O R C E M E N T



Thema: Konstruktion von Netzen mit REINFORCEMENT-Input,
die nur mittels der HEBB-Regel lernen.

Bearbeiter: Marcus Hutter MatNr.: 0893341

Betreuer: Gerhard Weiß

Abgabedatum: 2.7.90

0. Inhaltsverzeichnis

0. Inhaltsverzeichnis
1. Idee / Einleitung
2. Reinforcement-Hebb-Netze ohne Hidden-Units
3. Konstruktionsversuche von RH-Netzen mit Hidden-Units
4. Anmerkungen, Ausblicke
5. Literaturverzeichnis
6. Programmlisting
7. Protokoll eines einfachen Beispiels

1. Idee / Einleitung

Hier, in der Einleitung möchte ich die Idee, die hinter diesem Thema steckt, und das Thema selbst etwas näher erläutern. Dazu sei vorweg erwähnt, daß die meisten Vergleiche mit der Biologie und erst recht die Analogien zum Menschen recht spekulativ sind und nur zur Anregung dienen sollten.

zum Verständnis notwendige Grundkenntnisse

Übersicht über Netze - Gegenüberstellung

Aus zwei Gründen möchte ich zuerst eine kurze Übersicht über verschiedene Charakteristika neuronaler Netze geben. Da erstens die Vielfalt dieser Netze mit der Idee und damit dem Thema zu tun hat und zweitens ich einige darunter implementiert habe und die Auswahl anhand der Tabelle begründen möchte. Die Tabelle enthält nur die für diesen Artikel notwendigen Punkte.

Supervised <--> Unsupervised <--> Reinforcement
Backpropagation <--> Hebb-Lernregel
Statistische Units <--> Deterministische Units
Schwellwert Units <--> Sigmoid-Units
Synchroner Update <--> Asynchroner Update
Impuls-Units <--> Statischer Unit-Output

Idee

Supervised-Netze (z.B. mit Backprop.-Algorithmus) sind eine der erfolgreichsten Netze, haben aber den entscheidenden Nachteil ständig auf einen Lehrer angewiesen zu sein, der ihnen "sagt was zu tun ist". So ein Lehrer ist aber in vielen Problemen nicht verfügbar. Wesentlich bescheidener sind da die Reinforcement-Netze (nachfolgend kurz R-Netze), denen man nur "sagen" muß, ob ihre Reaktion richtig oder falsch war.
Dies entspricht in vieler Hinsicht auch mehr dem menschlichem Lernen durch 'trial and error'. Allerdings gibt es auch bedeutsame Unterschiede, die dieses Fopra anzupacken versucht. Ganz so sporadisch wie bei den R-Netzen ist die Rückkoppelung in der Natur nämlich nicht. Das R-Signal könnte man als das allgemeine Wohlbefinden des Individuums betrachten, welches es zu maximieren gilt. Doch dieses Signal wird weder ausschließlich noch direkt von der Umwelt geliefert. Vielmehr nehmen wir mehrere R-Signale in codierter Form über unsere normalen Sinnesorgane auf. Um etwas konkreter zu werden, gebe ich hier einige Beispiele:

zu helles Licht schmerzt in den Augen (R < 0)
gute Mahlzeit bekommt Zunge & Magen (R > 0)
Tritt ans Schienbein tut weh am Bein (R < 0)
heitere Musik erfreut das Gemüt (R > 0)

Ähnliche Beispiele lassen sich natürlich auch im technischen Bereich finden, etwa für einen Staubsauger-Roboter. Neurologisch scheint unser Gehirn noch weniger ein R-Netz zu sein, als vielmehr ein Unsupervised-Netz (nachfolgend kurz U-Netz), das wesentlich mit Hilfe der Hebb-Regel lernt. Doch unbestreitbar besitzen wir die Fähigkeit des R-Lernens. Die Punkte noch einmal zusammenstellend
ergibt sich die Frage: Wie kann ein Hebb-Netz R-Lernen ? Dies ist der Titel des Fopras.

Lösung

Obige Annahmen vorausgesetzt, hat es die Evolution anscheinend geschafft, aus einfachen U-Netzen durch Modifikation der Netzstruktur Rähnliche Netze zu konstruieren. Man kann dies auch anders sehen (vergleiche Kap. 3 in [2]): Der Lernprozess im Gehirn stellt auch eine Art Evolution auf einer kleinen Zeitskala dar (somatic time), die im Zuge der (darwinistischen) Evolution im großen Zeitraum von Jahrmilliarden (earth time) entstanden ist und immer mehr ausgefeilt wurde, sodaß heute "Lernen" auf zwei Zeitskalen stattfindet. Zuerst besaßen die Tiere nur fest verdrahtete Netze, dann U-Netze und irgendwann erfolgte der Sprung (oder eher der fließende Übergang) zu R-Netzen (und sogar zu S-Netzen). Einen solchen Übergang in einer (natürlich stark vereinfachten) Simulation festzustellen, weckte mein Interesse an Hebb-Netzen. Zuvor war es jedoch ratsam zu untersuchen, ob U-Netze überhaupt zu R-ähnlichen Netzen umfunktioniert (strukturiert) werden können, bevor man versucht, diese Aufgabe einem genetischen Algorithmus anzuvertrauen. Genau dies habe ich mit teilweisem Erfolg versucht:
Die (geschickte) Verschaltung von Hebb-Netzen zu R-ähnlichen Netzen, deren Details im folgenden näher ausgeführt werden. Der Ausspruch "Neurononale Netze programmiert man nicht, man konstruiert sie" spiegelt hier besonders deutlich die Verteilung des Arbeitsaufwandes wieder.

2. Reinforcement-Hebb-Netze ohne Hidden-Units

Eine einfache Klasse von Netzen sind Netze ohne Hidden-Units, die zwar nicht besonders leistungsfähig sind, aber sehr gut geeignet sind, Erfahrungen zu sammeln. Deshalb möchte ich diese Netzklasse hier näher untersuchen.
Bei solchen Netzen besteht nämlich kein prinzipieller Unterschied zwischen S- und U-Lernen. Beim S-Netz wird auf den Output der Output-Units gewartet und der Fehler der dabei gemacht wurde an die Output-Units angelegt und daraus die Gewichtsänderung berechnet (Backprop. entfällt bei 2 Layer Netzen). Bei U-Netzen mit nur sichtbaren Units (gleichzeitig Input- und Output-Units) werden beim Lernen verschiedene Muster angeboten und dadurch die Gewichte verändert. Anschließend werden nur noch Bruchstücke angelegt, deren Rest vom Netz rekonstuiert wird. Präsentiert man diesem U-Netz beim Lernvorgang ein Muster, dessen einer Teil dem Input des S-Netzes entspricht und dessen anderer Teil aus dem gewünschten dazugehörigen Output besteht und legt anschließend nur Teil 1 an, so wird das U-Netz Teil 2 rekonstruieren, ohne "zu wissen", daß wir dies als Output zu einem Input auffassen. Insofern ist die Unterscheidung in Output- und Input-Units nur Interpretationssache. Auf jeden Fall sind beide Algorithmen zur Gewichtsänderung in solchen Netzen äquivalent.
Ich verwende hier deterministische Schwellwert-Units mit Out- putbereich {-1,+1}, wobei ich häufig -1 als FALSE und +1 als TRUE interpretieren werde.

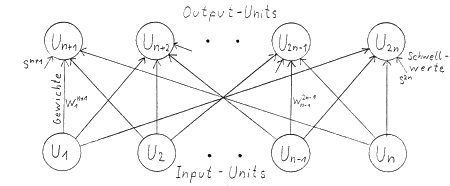
Zwei-Lagen-Netz ohne Hidden Units
Bild 1: Zwei-Lagen-Netz ohne Hidden Units


Grundkonstruktion

Das sichtlich einfachste Netz, welches man sich vorstellen kann, besteht nur aus je einer Unit im Input- und Output-Layer mit einem nach Hebb unsupervised zu lernenden Gewicht. Dies kann auch wie oben als S-Netz und sogar als R-Netz aufgefaßt werden, da hier die R-Information gleich dem Betrag der S-Information ist. Mit Hilfe dieser Information läßt sich aber der 'richtige' Output nach Tabelle 1 berechnen. R=-1 soll Bestrafung, R=+1 Belohnung bedeuten.

gelieferter Output -1-1+1+1
R-Info. -1+1-1+1
gewünschter Output+1-1-1+1
Tabelle 1: Berechnung des Outputs aus R-Info.

Dies ist die XNOR-Funktion. D.h. erweitere ich mein Netz um einen weiteren Input (dem R-Input), verknüpfe diesen mit dem Output des ursprünglichen Netzes zu XNOR, so erhalte ich den gewünschten Output, also einen Superviser. Die XNOR-Funktion läßt sich durch ein kleines Netz realisieren. Was fange ich aber in einem Hebb-Netz mit einem Superviser an ? Ganz einfach: Lege ich diesen mit einem sehr starken Gewicht als weiteren Input an die (einzige) Output-Unit, so erzwinge ich den erwünschten Output an der Output-Unit. Diese Situation unterscheidet sich nicht von derjenigen, in der ich direkt Input & zugehörigen Output an beide Units angelegt hätte (bis auf eine zeitliche Verzögerung). Dies ist aber genau die Situation im Unsupervised Fall - Und das Netz lernt diese IO-Kombination.

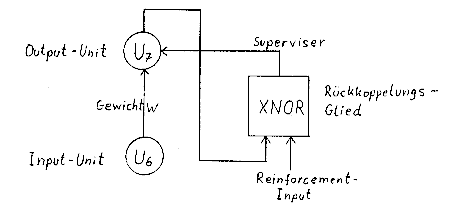
Erzeugung eines Supervisers (schematisch)
Bild 2 : Erzeugung eines Supervisers (schematisch)

Hier sind einige Bemerkungen angebracht: Bild 3 stellt unser Netz nun komplett dar. Die Units U1 bis U5 bilden ein XNOR-Gatter, wie man sich leicht überzeugen kann und sind wie oben beschrieben mit der Output-Unit U7 verbunden.

Einfachstes U-Netz mit R-Input
Bild 3 : Einfachstes U-Netz mit R-Input

Mit diesem Netz lassen sich zwei Funktionen lernen. Die Identität (Id) mit Gewicht größer Null bzw. die Negation (not) mit Gewicht kleiner Null. Überzeugen wir uns durch Analyse des zeitlichen Verhaltens, daß diese Funktionen bei geeignetem R-Signal tatsächlich auch gelernt werden (und nur in diesem einfachsten aller Beispiele ist dies überhaupt möglich). Nehmen wir an, das Netz soll ein 'not' lernen.
Der initiale Zustand der Units sei beliebig, am Eingang und am Ausgang liege eine 1. Dies ist nicht was wir wünschen, also legen wir am R-Eingang U5 ein negatives Reinforcement -1 an. Dieser wird nun mit dem Output von U7 XNOR verknüpft und gelangt nach 2 Zeitschritten (synchroner Update aller Units) nach U3 als eine -1. Ein kritischer Punkt ist, daß sich U7 in der Zwischenzeit geändert haben kann, z.B. auf -1. Dann wird aber das zeitlich korrespondierende R-Signal +1 angelegt (da dieser Output ja erwünscht ist), und dieses ergibt zusammen nach einer gewissen Verzögerung auch -1 an U3. D.h. in jedem Zeitschritt ändert sich der Input des XNOR-Gatters, der Ausgang liefert jedoch korrekt immer -1. Daß dieses 'Pipeline'-Prinzip funktioniert, ist nicht selbstverständlich und gilt auch nur bei Net- zen, bei denen für je zwei Units JEDER Weg zwischen diesen die gleiche Länge (d.h. gleiche Zahl an zwischen-Unit) hat, also bei streng geschichteten Netzen, wie das für dieses XNOR der Fall ist.
Nach zwei Zeitschritten liegt also an U3 der gewünschte Output an, unabhängig von der Netzinitialisierung, und wird im nächsten Schritt durch das starke Gewicht auf die Output-Unit U7 übertragen. Nun haben wir einen stabilen (und gewünschten) Output erreicht. In den ersten 3 Zeitschritten wird das Gewicht w aufgrund des zufälligen Outputs durch die Hebbregel zufällig verändert, also im schlimmsten Fall 3* um einen bestimmten Wert vergrößert, im Mittel einfach gleich gelassen. In den nächsten stationären Schritten, solange der Input noch konstant bleibt, wird das Gewicht garantiert verkleinert. Der Fall eines negativen Inputs verläuft analog und bewirkt letztenendes auch eine Verkleinerung von w. Damit konvergiert w gegen einen negativen Wert, der durch die Form der Hebbregel beschränkt bleibt. Dies stellt aber eine Negation wie gewünscht dar. In der anschließenden Rekapitulation des Gelernten, in der der R-Input auf einen beliebigen Wert >=0 gesetzt wird, wird durch die Rückkoppelung von U3 nach U7 der Output höchstens positiv, d.h. in gewünschter Weise beeinflußt. (darauf wird später noch eingegangen). Analog überzeugt man sich, daß bei umgekehrten R-Input wie erwünscht die Identität mittels positivem Gewicht w gelernt wird.
Dies ist das erste Hebb-Netz, welches zwei sich widerspechende Aufgaben lernen kann, einmal 'Id' und einmal 'not', in Abhängigkeit vom R-Signal.

Mehrere IO-Units

Vergrößern wir nun die Zahl der Input und Output-Units. Die Ersetzung einer Unit durch mehrere bedeutet einen qualitativen Sprung. Von mehreren zu noch mehr nur noch einen quantitativen, sodaß alles wesentliche schon an einem Netz mit je zwei Input- und Output-Units zu erkennen ist. Dazu kommen außerdem zwei zu lernende Schwellwerte (Bild 4).

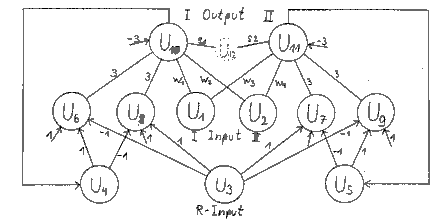
U-Netz mit R-Input, 2 Input-, 2 Output-Units
Bild 4 : U-Netz mit R-Input, 2 Input-, 2 Output-Units

Die Vermehrung der Input-Units bewirkt nur eine Verlangsamung der Lernrate. Für zwei Output-Units benötigen wir zwei XNOR-Rückkoppelungen. Da aber nur ein R-Signal zur Verfügung steht, das beiden zugeführt wird, können die an U10 und U11 erzeugten Werte nur noch im statistischen Mittel den gewünschten Output abgeben (positive Kovarianz; gleiches Phänomen wie beim Standard-R-Lernen). Damit wird eine direkte Verfolgung der Signale (mit der Absicht die Funktionsweise zu verstehen) unmöglich. Abhilfe schafft eine Tabelle, die für ein Beispiel angegeben ist.
U10 habe ein NAND, U11 ein OR zu lernen. Nur wenn beide Output-Units das richtige Ergebnis liefern sei R=1, ansonsten -1. Im allgemeinen wird das R-Signal den mittleren Fehlerabstand, normiert auf ein beliebiges Nullniveau darstellen, Feinheiten spielen für die Funktionstüchtigkeit nur eine untergeordnete Rolle. Legt man einen Input an, so gibt es 4 Output-Möglichkeiten des Netzes.

1. Beide Outputs sind (relativ zum gewünschten Output) falsch:
Das R-Signal wird -1 und nach 3 Zeitschritten zeigen die Output-Units gegenteiliges Verhalten, d.h. das gewünschte. Nun wird R=1 gesetzt und das System bleibt stabil.

2. Beide Outputs entsprechen dem gewünschten Output:
Das R-Signal wird +1 und der Zustand bleibt stabil.

3/4. Eine Unit liefert das richtige, die andere ein falsches Ergebnis:
Das auf -1 gesetzte R-Signal bewirkt eine Invertierung des Outputs. Dies führt aber wieder in den Fall 3/4. R bleibt -1 und die Outputs schwingen periodisch zwischen +1 und -1.

Im Fall 1 und 2 liefern die Output-Units den richtigen Wert, im Fall 3 und 4 zu 50% den richtigen und 50% den falschen Wert. Die Gewichtsänderung ist im Fall 3 und 4 also 0, da sich positive und negative Kovarianzen aufheben. D.h. nur Fall 1 und 2, die beide (spätestens nach einer Verzögerung) den gewünschten Output liefern, tragen zum Lernen bei. Bei geringsten Unregelmäßigkeiten im Update der Units im Fall 3/4 (also speziell bei asynchronem Update) geht dieser oszillierende in den stabilen Zustand 1/2 über. Somit ist die Abschätzung, daß in 50% der Fälle, also 50% der Zeit, effektiv gelernt wird, im allg. zu schlecht.
In Tabelle 2 ist zu jeder stabilen IO-Kombination die zugehörige und in der letzten Spalte die mittlere Gewichtsänderung angegeben. Die Zahlenwerte bedeuten, daß bei unendlich langer Verweilzeit in diesem Zustand die Gewichte gegen +-1 konvergieren würden, bei zyklischer Repräsentation der Inputs gegen +-<1.

Input I -1 -1 +1 +1
Input II -1 +1 -1 +1
Output I +1 +1 +1 -1 W
Output II -1 +1 +1 +1
Gewicht W11 -1 -1 +1 -1 -«
Gewicht W21 -1 +1 -1 -1 -«
Schwellwert S1 +1 +1 +1 -1 +«
Gewicht W12 +1 -1 +1 +1 +«
Gewicht W22 +1 +1 -1 +1 +«
Schwellwert S2 -1 +1 +1 +1 +«
Tabelle 2: Gewichtsänderung im 2-2 Netz

Wie man sich leicht überzeugen kann sind die zur korrekten Funktion des Netzes notwendigen Gewichte und Schwellwerte gerade die in der Tabelle angegebenen. Das Netz lernt also kor- rekt. Dies gilt für alle Paare von boolschen Funktionen, solange diese nicht XOR oder XNOR sind, welche prinzipiell nicht durch ein Netz ohne Hidden-Units dargestellt werden können (Siehe Kapitel 3)

Größeres Beipiel

Wie oben schon erwähnt, läßt sich die Argumentation auch auf größere Netze übertragen. Um ganz sicher zu gehen, ist es am besten einfach ein größeres Netz zu konstruieren und zu testen. Dabei nimmt die Lernzeit allerdings schneller mit der Anzahl der Output-Units zu (exponentiell ?) als dies theoretisch notwendig wäre (linear !). Auch wird im allg. nicht mehr fehlerfrei gelernt, alles in allem ergeben sich aber durchaus zufriedenstellende Ergebnisse (wenn man die Einfachheit der Mittel berücksichtigt).

Anmerkungen

3. Konstruktionsversuche von RH-Netzen mit Hidden-Units

Um es gleich vorwegzunehmen - der Versuch, die Idee aus Kapitel 2 auf Netze mit Hidden-Units, um die es in diesem Kapitel geht, zu übertragen, ist gescheitert. Welche Probleme dabei auftraten und die Versuche, diese zu lösen, sollen im folgenden erörtert werden. Der Einfachheit halber beziehen sich die meisten nun folgenden Betrachtungen auf Netze mit nur einem Hidden-Layer (ähnlich Bild 5). Es wurden alle Experimente mit durchgeführt.

Erweiterte Klasse von Netzen

Stellt man sich das Input-Layer der bisher betrachteten 2-Layer-Netze als Hidden-Layer-Schicht vor, die von anderen Units durch Verbindungen mit festen Gewichten gespeist werden, so ändert dies natürlich weder am Lern-Prinzip, noch am Rückkoppelungsmechanismus etwas, d.h. auch solche Netze können R-Lernen. Anders interpretiert stellen diese Units Hidden-Units mit von vornherein durch die Netzstruktur festgelegter Bedeutung dar, und stellen somit keine 'echten' Hidden-Units dar. Man kann theoretisch durch eine solche feste Zwischencodierung zwar alle Probleme auf lineare Probleme reduzieren und damit auf die hier beschriebene Weise lösen, doch nimmt die Zahl der benötigten Hidden-Units exponentiell (also unbrauchbar) mit der Zahl der Input-Units zu. Für zwei Input-Units benötigt man 2ý=4 Hidden-Units. Somit hat ein Netz, das neben den 14 Bool-Funktionen auch XOR und XNOR lernen kann, folgende Gestalt.

Netz, das alle 16 bool.-Funtionen lernen kann
Bild 5: Netz, das alle 16 bool.-Funtionen lernen kann

Diese Methode ist für große Netze aber absolut unbrauchbar und führt an der Idee der Hidden-Units total vorbei.

Rückkoppelungsverzögerung bei Hidden-Units

Eine 'echte' Hidden-Unit, deren Bedeutung erst gelernt wird, besitzt mindestens eine flexible Verbindung inputseitig. Die naheliegendste Idee ist, auch solche Units mit einem XNOR-Rückkoppelungsglied zu verbinden. Die Argumentation könnte etwa wie folgt aussehen:
Jede Hidden-Unit trägt zu einem gewissen Prozentsatz zum Output bei, d.h. es wird eine positive Korrelation zwischen der Korrektheit der Hidden-Unit und der Output-Unit und somit auch zum R-Signal bestehen.
Folgendes muß jedoch im Fall des synchronen Updates unbedingt beachtet werden: Ein Output einer Hidden-Unit beeinflußt erst im nächsten (bzw. nächsten n) Schritt den Netz-Output und damit das dazugehörige R-Signal mit dem er durch die XNOR-Rückkoppelung verbunden wird. Der Output der Hidden-Unit muß somit einen (bzw. mehrere) Schritte 'aufbewahrt werden' bevor er mit dem R-Signal verknüpft werden kann. Diese Aufbewahrung kann durch eine zwischen Hidden-Unit und XNOR-Eingang geschaltete Unit bewerkstelligt werden. (Das Problem der zeitlichen Nicht-lokalität haben viele Netze). Allen Versuchen zum Trotz stellte sich nicht einmal bei einfachsten nicht-linearen Problemen (XOR) ein Lernerfolg ein.

Schwacher Feedback für partiell korrekte Funktionen

Da auch eine Hidden-Unit mit XNOR-Rückkoppelung versucht die gestellte Aufgabe 100% korrekt zu lösen, dies aber aufgrund der Art der Aufgabe nicht möglich ist, sollte sie diese wenigstens partiell korrekt lernen, sodaß in der nächsten Schicht aus den partiell korrekt gelösten Aufgaben der Hidden-Units die exakte Lösung in der 2. Schicht linearkombiniert werden kann. Nun stellte sich aber bei 2-layer Netzen heraus, daß diese bei dem Versuch ein XOR zu lernen, lieber gar nichts lernten, als ein OR, NAND oder etwas ähnlichem, welche aber typische Kandidaten für eine interne Repräsentation/Codierung und anschließender Linearkombination zu einem XOR sind. Abhilfe schafft hier, die Zwangsrückkoppelung von U3 nach U7 in Bild 1 und analog in allen anderen abzuschwächen (Werte kleiner 1), um so dem Netz die Möglichkeit zu geben, entgegen seiner Vorbestimmung zu reagieren. Tatsächlich lernten die Netze weiterhin die auch theoretisch erlernbaren Aufgaben; bei nichtlinearen Aufgaben wurden Approximationen gelernt. Leider führte auch diese Modifikation in Multilayer-Netzen nicht zum Erfolg.

Feedback zu jedem 2. Layer

Ein Problem war folgendes: Da sowohl Output-Layer als auch Hidden-Layer bei negativem Reinforcement zu inversem Verhalten gezwungen werden, ändert sich am Produkt ihrer Aktivationen ((-a)*(-b)=a*b) und damit an der Richtung, in der die Gewichte geändert werden, nichts. Nur zwischen Input- und erstem Hidden- Layer ändert sich das Vorzeichen und der Rückkoppelungsmechanismus 'greift'.
Dem könnte Abhilfe geschaffen werden, indem nur jede 2. Netzschicht rückgekoppelt wird und damit die Lernrichtung bei negativem Reinforcement in jedem Layer umgekehrt wird. In einem 3-Layer-Netz bedeutet dies, nur die mittlere Schicht rückzukoppeln. Wie auch bei allen anderen Modifikationen brachte dies zwar eine konvergenzfördernde Wirkung, aber keineswegs eine befriedigende.

Symmetrische Gewichte

Ersetzt man im Netz die Gewichte durch symmetrische, d.h. fügt Gewichte gleicher Stärke und Flexibilität in entgegengesetzter Richtung hinzu, und betrachtet sowohl Input- als auch Output-Layer als Inputs, so hat man ein unsupervised lernendes Netz mit Hidden-Units. Hätten sich nicht schon bei dieser Lernmethode unlösbare Schwierigkeiten ergeben, wäre der Versuch, nun die Information am Output-Layer durch eine XNOR-Rückkoppelung mit R-Signal zu approximieren, einer der erfolgsversprechendsten gewesen. Da mir aber kein funktionsfähiges Hebb-Netz mit Hidden-Units bekannt war, konnte ich die Fehlerursache nicht finden.

Boltzmann-Netze

Das passendste, das ich finden konnte, waren Boltzmann-Netze, die von der Idee der Hebb-Netze nicht allzuweit entfernt sind. Die Gewichtsänderung ist im wesentlichen wie bei Hebb-Netzen proportional zur Korrelation benachbarter Unit-Aktivitäten. Die Unterschiede zu Hebb-Netzen sind folgende: Da aber beide Unterschiede über den Rahmen der üblichen Hebb-Netze hinausgehen und mir keine funktionsäquivalenten Simulationen innerhalb dieses Rahmens eingefallen sind, führte jene Entdeckung nur zur Erkenntnis, daß der Rahmen (Hebb-Netze) vielleicht enger als notwendig gesteckt war (Siehe Kap. 4).

Einfluß der Musterrepräsentationshäufigkeit auf die Gewichte

Beim Versuch, die verschiedenen Inputmuster nicht mehr gleichhäufig zu präsentieren, zeigte sich eine auffällige Abhängigkeit der Gewichte hiervon. Diese an sich negative Erscheinung, die auch bei vielen anderen Netzen zu finden ist, konnte an dieser Stelle gewinnbringend eingesetzt werden. Präsentierte man dem Netz Muster, die es gut gelernt hatte, seltener, noch unzureichend gelernte entsprechend häufiger, so ließ sich der Lernvorgang bei 2-Layer Netzen aus Kap.2 beschleunigen. Bei einem 3-Layer-Netz mit 2 Hidden Units ließ sich unter anderem folgendes Problem lösen: Versucht man einem 3-Layer-Netz bei gleichverteilter Präsentationshäufigkeit ein XOR zu lernen, so ist der Output zu 50% 1 und zu 50% -1, d.h. der Schwellwert der Output-Units wird gegen 0 konvergieren. Mit einem solchen Schwellwert ist es aber unmöglich ein XOR zu lernen. Legt man die Muster aber in oben beschriebener Weise an, so konvergiert zumindest der Schwellwert gegen den benötigten Wert (abhängig vom Verhalten der Hidden-Units).

4. Anmerkungen / Ausblicke

Man kann sich fragen, woran es wohl gelegen haben kann, daß alle Konstruktionsversuche von RH-Netzen mit Hidden-Units gescheitert sind. Liest man Kapitel 3 sorgfältig, so stellt man fest, daß an einigen Stellen erfolgversprechende Versuche hätten durchgeführt werden können, wenn man die Beschränkung auf Hebb-Netze aufgehoben hätte. Doch stellt sich dann die Frage, "wie weit man geht". Schließlich ist es kein Problem mit 'beliebigen' Units (nämlich R-Units) R-Netze zu konstruieren. Aus dieser Perspektive war ein eindeutig definierter Rahmen für die Charakteristika der Units durchaus sinnvoll. Doch scheint dieser Rahmen zu eng gewählt worden zu sein, aber jede Erweiterung 'im nachhinein' gekünstelt.
Konzentriert man sich dagegen auf die Idee des impliziten Reinforcement (Erklärung siehe Einleitung), so kann man, da dieses Problem meines Wissens noch niemand untersucht hat, auf einen abgrenzenden Rahmen verzichten. Läßt man gleich einen genetischen Algorithmus an dieses Problem, ohne Voruntersuchungen ähnlich zu meinen anzustellen, dann ist eine erfolgreiche Evolution eines Netzes mit implizitem R-Signal auch dann noch beachtlich, wenn man beliebige Units zuläßt. Auch die Verwendung von verschiedenartigsten Units innerhalb eines Netzes könnte für die Evolution von Vorteil sein.
Insgesamt glaube ich, daß mit den heutigen Erkenntnissen und Mitteln, eine solche 'Evolution von (implizitem) Reinforcement', nachgebildet (simuliert) werden kann. Dies wäre auch ein experimenteller Beweis dafür, daß evolutionäre Prozesse auf einer Langzeitskala Lernverfahren auf einer Kurzzeitskala hervorbringen können.

5. Literaturverzeichnis

Literatur zum Fopra

[1] Williams R.J.; 1988 Toward a theory of reinforcement learning; Techn. Report NU-CCS-88-3, College of Computer Science, Northeastern Univ. (Boston)
[2] Gerhard Weiss: 1990 Combining neuronal and evolutionary learning; Techn. Report FKI-132-90; TU-München; weissg@tumult.informatik.tu-muenchen.de
[3] Hinton G.E & Sejnowski T.J.; 1986; Learning and relearning in Boltzmann machines; IN: [5], Chapter 7, pp. 282-317
[4] Schulten K.; 1986 Associative Recognition and Storage in a Model Network of Physiological Neurons. IN: Biological Cybernetics 54,319-335 1986; Springer-Verlag

Allgemeine Literaturhinweise

[5] Rumelhart D.E. & McClelland J.L.; 1986; Parallel distributed processing vol 1 & 2. Book/MIT Press
[6] Goldberg D.E.; 1989; Genetic algorithms in search, optimization machine learning; Addison-Wesley

 © 2000 by ... [previous] [home] [search] [science] [calculators] [personal] [contact] [up] [next] ... Marcus Hutter